第二章 小牌体系
什么是小牌体系
什么是小牌体系
对这个问题标准的回答当然是:
但是我们还需要一个不同的定义——比上面的回答更贴近现实。
- 小牌指的是任意一张牌,可以将它和同花色中的其它小牌交换而不影响该花色的打牌情况。
这个定义不同于“小牌”和“大牌”字面上的意思,而从下面的角度来看问题:
- 小牌的等级跟它获取赢墩的能力无关
- 大牌的等级,恰恰相反,跟它获取赢墩的能力紧密相关
用一些例子来进一步说明:
假设花色分布如下:
所有Q以下的牌张都是小牌。它们中的任何两张牌都可以互换位置而不影响最后的结果:南北方得到全部的4墩牌。因此
这个局势可以被简化为:
每一张小牌都用符号“x”来表示,因为它的等级是无关紧要的。
但在下面这个例子里:
小牌指的是比8小的牌。9和8在这个例子里不是小牌,因为如果把西的9和南的3交换并由东引牌,或把东的8和南的3交换并由西引牌的话,南北方都
能够获取4墩牌。因此这个局势的简化图如下:
小牌的性质
把上面的例子和我们对小牌的定义结合起来,可以看到如下事实:
- 小牌和大牌之间没有明确的分界,和该花色的特定分布紧密相关
- 所有的小牌都等价
什么是有效小牌
一个有点令人难堪的事实是:你一开始随手垫掉了一张小牌,而在后面的打牌进程中发现它本可以为你带来一个赢墩。
所以让我们定义“有效小牌”为那些有可能成为大牌的牌张(即使形式上它是一张小牌)。很明显,等级越高的小牌成为
“有效小牌”的几率也越大。
小牌作为信息源
再来看另一个事实:当你决定在某一墩牌上打出一张小牌时,初看上去你出哪张牌都无所谓,反正它都无法给你带来赢墩。
然而,每张小牌都各自拥有不同的号码,并且可以因此而被区分开来。很自然地我们会问——应该怎样对每张小牌的独一无二性
加以利用呢?答案很简单:传递信息。比如跟出这门花色最小的小牌而非最大的小牌;或者我们以从小到大而非从大到小的顺序跟出
手中的小牌,同伴都可以从中推断出某些结论。当然,要实现这一点,搭档间必须事先商定好每个信号的含义。
什么是小牌体系?
只要你愿意,小牌可以传递任何种类的信息,比如牌型分布,手中AK的数量,甚至高花中有几张牌等等。然而在这里
我们不会去讨论这些有趣的可能性;本书关注的是一个基本的防御问题:
任何试图做到这一点的方法都可以被称之为“小牌体系”。我们将分析一些传统小牌体系,并试图发现最优的体系。注意:
第一章里提到的普遍假设在这里仍然是正确的。
信息的准确性
让我们先来决定,就花色的长度和质量而言,如何才称得上是准确的信息传递。
长度
在实战中,通过分析可见的26张牌(明手+你自己),以及叫牌和打牌的过程,绝大多数情况下你都能大概知道定约人的各门花色长度。
一个有经验的牌手会知道(并且很少出错),在某门特定的花色中:
- 定约人有0或1张牌
- 定约人有1或2张牌
- 定约人有2或3张牌,等等
如果他可以对定约人的牌做如此推理,同理他也能对同伴的牌这么做。因此假如我们能告诉同伴自己在这门花色
中的长度是奇数还是偶数,则信息的传递就已经很充分了。他可以通过分析可见牌张以及叫牌和打牌过程来判断
定约人的确切长度。
长度问题
根据上面的推理过程我们可以把防御问题分为以下几类:
举例来说,如果同伴已知你在某花色中有3-4张牌,我们就用问题3-4来指代这个防御局势。
质量
很明显,长度不是唯一重要的因素。花色的质量(大牌的张数)同样很重要。经验表明同伴无法通过已有的信息
(明手,他手中的牌,还有叫牌和打牌过程)来确定你首攻花色的质量,因此你必须通过事先商定好的协议用
小牌信号来帮助他。鉴于你持有两个及以上大牌的可能性很小(主打方通常拥有较多的大牌),而且试图告诉
同伴你具体是哪一张大牌是几乎不可能的,你应该满足于告知同伴你的套是坏套(全部由小牌组成),还是好套
(包含一张任意大牌)。
信息的类型
迄今为止我们单独划分出了两种类型的信息:
这意味着4个基本可能性:
-
花色长度是偶数,没有大牌
-
花色长度是偶数,有一张大牌
-
花色长度是奇数,没有大牌
-
花色长度是奇数,有一张大牌
下面是对问题3-4(同伴知道你在该花色中有3-4张牌)的所有可能性列表:
| |
质量 |
| 长度 |
坏 |
好 |
| 偶数 |
xxxx |
Hxxx |
| 奇数 |
xxx |
Hxx |
上面表格中的“x”代表小牌,而“H”代表大牌。
信号
毫无疑问,如果能告诉同伴你的确切持牌是“xxx”或者是“Hxx”当然是最好不过了。但让我们此刻暂时不去想这个
宏伟的目标,而先着重于解决一个相对来说容易一点的任务:告诉同伴“我有xxx或Hxx”或者“我有xxx或xxxx”
诸如此类比较模糊的信息。有多少种方法能实现呢?下面这个对问题3-4的图解将告诉我们答案。
如上图所示有3种可能的方法,我们称之为信号。
-
长度信号(L):告诉同伴关于张数的信息
-
奇数 = xxx 或 Hxx
-
偶数 = xxxx 或 Hxxx
-
质量信号(Q):告诉同伴关于花色质量的信息
-
坏 = xxx 或 xxxx
-
好 = Hxx 或 Hxxx
-
混合信号(M):告诉同伴混合信息
-
? = Hxx 或 xxxx
-
? = xxx 或 Hxxx
混合信号
长度信号和质量信号都是传统性质的信号——已经被人们熟知和使用了很长时间。然而混合信号,则是来自纯理论分析的结果。为了证明它
的有效性我们必须回答下面两个问题:
-
什么是“混合”信息?
-
它在实战中有何用途?
混合信号告诉同伴你手中究竟有几张小牌:
-
偶数 = Hxx 或 xxxx
-
奇数 = xxx 或 Hxxx
对第二个问题,最好用一些实例来进行阐明。
问题3-4:
西首攻一张小牌来对抗花色定约。东用A赢得第一墩后回出同一花色,定约人K吃进。当东家再一次进手后,他
将面临如下问题:如果西家在该花色的原始持牌是Qxx,他们就还有一墩牌可拿;而如果西原本持有xxx或Qxxx
的话防守方就必须从别的地方去找赢墩。很显然在这里长度信号或质量信号都帮不上忙,因为即使你知道西
的原始长度是3张,它们也可能是xxx三张小牌;而就算你知道西持有Q,他也可能持有Qxxx四张。在这个局势下
只有混合信号才是有效的。
再来看一下问题2-3:
对抗花色定约,西首攻一张小牌,东出Q,被南的A赢进。当东家再次上手后(比如说用王牌A),他现在处于困境
中:如果西持xx,就可以给他一个将吃;如果西持Jxx,防守方可以再拿两墩牌;如果西持xxx的话,甚至于兑现
K都是很危险的,因为明手的第4张小牌将被树立为赢墩。这再一次说明,只有混合信号才能起作用,因为东家知道
西的牌要么是“xx或Jxx”(偶数张小牌),要么是“xxx”(奇数张小牌)。
如果首攻就能传递这一信息是再好不过的了。
最后让我们来检查问题4-5:
西从A10xx中引小牌来对抗无将定约,南让明手出Q并赢得这一墩。当西再次进手后,当首攻花色是 时
他应该续拔A;当首攻花色是
时
他应该续拔A;当首攻花色是 时他应该寻找同伴的进手;当首攻花色是
时他应该寻找同伴的进手;当首攻花色是
 时他可以随意引一张牌。只有在东家的小牌是如下的混合信号时西才
能做出正确的决定。
时他可以随意引一张牌。只有在东家的小牌是如下的混合信号时西才
能做出正确的决定。
-
偶数张小牌 = Jxxxx 或 xxxx
-
奇数张小牌 = Jxxx
最后要说的是,当定约人在该花色中的大牌已知的话,混合信号自动转变成简单的长度信号;同样的,当定约人
的花色长度已知的话,则混合信号自动转变成简单的质量信号。
对信号的评估
让我们检查三种信号所传递的信息量,从而对它们进行合理的评估。再来看看4种基本可能性的图解:
每个信号表示同伴有两种可能的持牌情况,而能把它们区分开来的机会也跟牌情本身的差距成正比。因此
我们需要检查6个信号(L0,L1,Q0,Q1,M0,M1),
并按容易区分牌情的程度对它们进行排序,由此来评估每个信号的好坏程度。
质量信号(Q)表示同伴有两种牌情:
-
Q0 = xxxx 或 xxx
-
Q1 = Hxxx 或 Hxx
两种情况是相同的,换句话说,不管你是拿掉一张小牌还是增加一张小牌,区分这两种牌情的难易程度不会改变。
因此我们得出:Q0 = Q1
长度信号(L)表示同伴有两种可能持牌:
-
L0 = Hxxx 或 xxxx
-
L1 = Hxx 或 xxx
两种情况仍然相同;不管我们是把一张大牌换成一张小牌还是反过来,这意味着:L0 = L1
混合信号(M)表示同伴的牌情可能是:
-
M0 = Hxx 或 xxxx
-
M1 = Hxxx 或 xxx
在这两种情况里:
-
M0 = 把一张大牌换成两张小牌
-
M1 = 去掉一张大牌
因此我们有以下4种不同类型的信号:
-
Q = 去掉一张小牌
-
L = 把一张大牌换成一张小牌
-
M0 = 把一张大牌换成两张小牌
-
M1 = 去掉一张大牌
要想数字化地地描述这4种类型,我们必须先建立起一张大牌和一张小牌的相对价值。根据过往经验以及数据支持
(比如4张xxxx的将牌支持略强于Hxx,而略弱于HHx),让我们做如下假设:1½张小牌 <= 大牌 <= 2张小牌。
因此我们有:
-
小牌的价值 = 1
-
大牌的价值 = 1 + δ,此处½ <= δ <= 1
两种可能牌情之间的差距越大,则信号传递的信息价值也越高。注意到1 − δ <= δ <= 1 <= 1 + δ,
我们得出4种信号的价值由小到大顺序为 M0 <= L <= Q <= M1。
从以上的分析可以看出,很多人认同的长度信号绝对优于质量信号的观点并不是正确的。
下面是一个图形化的演示:
让我们转化成百分比来看看。假设:
-
δ = ¾(最可能的取值)
-
最差的信号(M0)的价值是50%
-
最好的信号(M1)的价值是68%(为什么?)
-
信号的价值和它代表的两种牌情之间的差距成正比
我们得到:M0 = 50%;Q = 56%;L = 59%;M1 = 68%
信息的来源
现在我们已经大概知道了需要传递什么样的信息,下面要讨论的就是传递信息的方法。
头两墩牌
我们只在某特定花色的头两墩牌上传递信号,因为到第三轮出牌的时候该花色的情况就已经基本明了了。
这两墩牌并不需要是连续打出的;它们之间可以相隔一轮或多轮其它花色的出牌。
用小牌传递信号的关键
我们不能用特定的小牌来表达某种特定的含义,比如我们不能说首攻3表示自己持有Hxx,或首攻7表示
持有xxx或xxxx等等,因为这种方法成立的前提是你持有这张牌。唯一有意义的方法是根据小牌的等级
来安排你的首攻。当你持有3张小牌时,不管他们的号码如何,里面总有一张是最大的,一张位于中间,
而一张最小。因此我们可以规定当从xxx中首攻时我们出最大牌,从Hxxx中首攻时引中间小牌,从Hxxxx中
首攻时引最小牌,等等。
符号标记法
为了简化方法的描述我们假设小牌的写法是从左到右降序排列,也就是说:
-
Hxx = H73 或 H62 或 H85 等等
-
xx = 64 或 52 或 43 等等
-
Hxxx = H642 或 H853 或 H954 等等
我们用圆圈代表首攻的小牌,而箭头的指向代表第二墩出的小牌,例如:
-
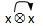 表示当持3张小牌时,我们先攻
中间张,然后再出最小张
表示当持3张小牌时,我们先攻
中间张,然后再出最小张
-
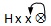 表示当持带一大牌的4张套时,
我们先攻最小的小牌,然后再出中间的小牌
表示当持带一大牌的4张套时,
我们先攻最小的小牌,然后再出中间的小牌
对小牌体系的正式定义
现在我们可以给小牌体系一个正式的定义——搭档间协议好的各种小牌序列组合的出牌方法:xx,Hxx,
xxx,Hxxx,xxxx等等。
出牌的选择
上面讨论过的每种信号都代表着两种牌情:
-
长度信号 = 偶数或奇数张
-
质量信号 = 好套或坏套
-
混合信号 = 偶数或奇数张小牌
让我们来考虑怎样发出信号才能分辨这两种情况。如果我们想要在该花色的第一轮出牌上就做到这一点,
那么最好的方法就是出最大的小牌或者最小的小牌。然而,如果我们可以通过前两轮出牌来实现这个目标的
话,最佳途径是按升序或降序来跟出手中的小牌张。在这里升序的意思是第二轮出的小牌号码大于第一轮
出的小牌,而降序则正好反过来。
各种选择的符号标记
在描述各种选择时我们使用如下符号:
-
↑ = 打出最大的小牌
-
↓ = 打出最小的小牌
-
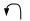 = 以升序方式打出小牌
= 以升序方式打出小牌
-
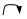 = 以降序方式打出小牌
= 以降序方式打出小牌
一些例子:
-
持Q75时符号 ↑ 表示出7
-
持982时符号 ↓ 表示出2
-
持Hxxx时符号
 表示可能是
表示可能是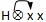 ,
,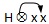 ,或
,或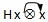 中的一种
中的一种
-
持A8542时符号
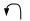 表示可能是
表示可能是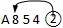 ,
,
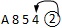 ,
,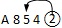 ,
,
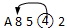 ,
,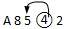 ,
或
,
或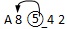 中的一种
中的一种
这些符号非常清楚并且容易记忆。
各种选择的信息源
各种选择的信息来自下面列出的资源:
-
资源F = 第一张小牌(First small card),可以是最大张(↑),也可以是最小张(↓)。
-
资源O = 小牌的次序(Order of small cards),可是是升序(
 ),也可以是降序(
),也可以是降序( )。
)。
-
资源S = 第二张小牌(Second small card),可以是最大张(↑),也可以是最小张(↓)。
一定要牢记每张小牌自身并不重要,重要的是用它的等级来传递信息。
对信息源的评估
让我们简要地评估一下三种已知信息源:
-
资源F(第一张小牌)。信息可以快速传递,但并不可靠,因为很多时候并不清楚同伴出的是↑还是↓。
-
资源O(小牌的次序)。信息可靠,但速度偏慢(必须要等到该花色的第二墩牌才能确认)。然而,
我们有可能推断出第一张小牌是↑还是↓。
-
资源S(第二张小牌)。毫无疑问这是最差的信息源,因为它既不可靠又慢。当然实际情况并不如我们
想象的那么差,因为在第二轮上已经有相当多的小牌被打出了。
如你所见,没有一种信息源是理想的:
-
F 速度快但是不可靠
-
O 可靠但是速度偏慢
-
S 既不可靠又速度偏慢
信号的传递
每种信号(L,Q,和M)都在传递两种不兼容的牌情之一,让我们称之为A和B。举个例子:
每个信息源(F,O和S)以两种不同的方式来传递信息:
-
对信息源F和S来说,出 ↑ 或 ↓
-
对信息源O来说,出小牌的次序是
 或
或
为了从某个信息源发出信号,我们当然必须事先决定两种不兼容的牌情对应哪种信号。比如,我们可以说:
| 对信息源F或S来说 |
对信息源O来说 |
| ↑ 代表牌情 A |
 代表牌情 A 代表牌情 A |
| ↓ 代表牌情 B |
 代表牌情 B 代表牌情 B |
上面表格中每个符号的含义可以进行对调(比如↑ 代表B而 ↓ 代表A),而理论上两种方法产生的效果应该是相同的。由此我们得出的结论是每种信号
(不管使用何种信息源)都可以用两种方式来传递信息,让我们称其中的一种为常规信号,而另一种为反式
信号。
常规信号(经典方式)
常规长度信号(L):
-
↓ 或
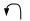 表示该花色是奇数
表示该花色是奇数
-
↑ 或
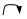 表示该花色是偶数
表示该花色是偶数
常规质量信号(Q):
-
↓ 或
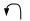 表示好套(有一个大牌)
表示好套(有一个大牌)
-
↑ 或
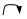 表示坏套(都是小牌)
表示坏套(都是小牌)
常规混合信号(M):
-
↓ 或
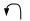 表示该花色有偶数张小牌
表示该花色有偶数张小牌
-
↑ 或
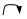 表示该花色有奇数张小牌
表示该花色有奇数张小牌
上面描述的信号方法在本书中将被称之为常规或经典信号体系,我们用符号L Q M来分别指代它们。其中L和Q已经被人们所熟知
并使用了很长时间,完全担得上“经典”二字的评语。方法M则是一个全新的信号体系,还没有很长的历史,但
我们也把它归入常规体系,以区别下面将要讨论的反式体系。
反式信号
反式长度信号(L*):
-
↓ 或
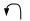 表示该花色是偶数
表示该花色是偶数
-
↑ 或
 表示该花色是奇数
表示该花色是奇数
反式质量信号(Q*):
-
↓ 或
 表示坏套(都是小牌)
表示坏套(都是小牌)
-
↑ 或
 表示好套(有一个大牌)
表示好套(有一个大牌)
反式混合信号(M*):
-
↓ 或
 表示该花色有奇数张小牌
表示该花色有奇数张小牌
-
↑ 或
 表示该花色有偶数张小牌
表示该花色有偶数张小牌
我们用符号L* Q* M*来分别代表它们。
常规还是反式?
理论上来说,这两种方法应该是等价的。但在实战中,常规信号通常较优;举例来说,如果你持HXX,
稍大的那张小牌有可能会是一张有效小牌,因此最好不要在第一墩牌上就打出做信号之用。
哪种质量信号才是经典方式?
常规质量信号(↓ 或  = 好套)在实战中的应用如下:
= 好套)在实战中的应用如下:
换句话说:
读者可能会对作者把这种方法称之为“常规”信号有点迷惑不解,因为流行的术语称之为“反式”。然而,有必要
注意到这种处理是和克伯森的小牌体系一致的,该体系:
-
从全是小牌的花色中引牌时,出最大的那张小牌
-
从一张大牌领头的花色中引牌时,出最小的那张小牌
从这个角度来看“↓ 或  = 好套”
的存在时间更长,因而更值得被称为“常规”信号。而现实中人们没有这么做可能是由于历史上的误解造成的。
= 好套”
的存在时间更长,因而更值得被称为“常规”信号。而现实中人们没有这么做可能是由于历史上的误解造成的。
造成误解的原因——鼓励
为了更好的理解为什么“↑ = 好套”被广泛地认为是“常规”信号,让我们假定你正在用经典的克伯森方式来
防御一个花色定约,同伴首攻K(显示AK或KQ)。从如下三种持牌中你应该分别打哪张小牌:
由于你是采用经典方式进行首攻,为方便起见在跟牌时最好也采用相同的信号,也就是说“低级的小牌 = 好套”,
你应该跟出:
然而,这么跟牌的后果是同伴无法区分你到底是双张还是3张小牌。也许你应该用常规长度信号(
低级的小牌 = 奇数张)更好:
但同样还是有问题,因为现在同伴无法区分你到底是3张小牌还是3张带Q。因此对于这类局势不管是
常规质量信号还是常规长度信号都无法起作用(对反式信号也是如此)。为了解决这个问题,人们引进了
鼓励信号:当同伴首攻一门花色的时候,你跟出的一张小牌意味着:
由于人们的直觉认为号码较大的小牌 = 鼓励,号码较小的小牌 = 消极,下面这个鼓励信号产生了:
在长时间的使用后,这个方法被称之为常规(经典)信号。相应地,由于在持有一个大牌时鼓励的情况
远远多于全是小牌时的情况,人们进一步认为“↑”对应的是“好套”而把其命名为常规信号,虽然在更经典的
小牌体系中“↑ = 坏套”。最后要强调一点,“↓ = 鼓励”其实是更好的方法,因为当你持有一张大牌时,
较大的小牌成为有效小牌的机会要高一些,也基于此原因更应该被称之为常规信号。
小牌体系的定义
有两种方式来定义小牌体系:
正式的定义
这个定义运作的方式是对每一种特定的持牌都事先商定好出牌的次序(第一墩和第二墩):
| xx |
|
| xxx |
Hxx |
| xxxx |
Hxxx |
| xxxxx |
Hxxxx |
| xxxxxx |
Hxxxxx |
例如: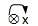 ,
,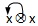 ,
,
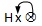 ,
, ,
,
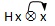 ,
,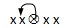 等等
等等
这种定义方式能够让你描述任何一种小牌体系,亦即普适定义。然而同时它也是相当无趣的,因为它没有深入
探讨打出的每一张牌的含义,仅仅给出一个正式的描述。
结构性定义
这种定义方法从3种信息源之间的相互作用入手来描述小牌体系。我们有F,O,S三种信息源和6种可能的信号:
| |
常规 |
反式 |
| 长度 |
L |
L* |
| 质量 |
Q |
Q* |
| 混合 |
M |
M* |
我们首先必须建立一些映射关系,即那种信息源传递何种信号。这意味着一个小牌体系可以被描述成三方综合体:
SF SO SS
-
SF = 由信息源F传递的信号
-
SO = 由信息源O传递的信号
-
SS = 由信息源S传递的信号
举例来说:LQM,QQL*,ML*Q,Q*MM,QL*M,M*M*L 等等。
信息源之间的相互作用
粗看上去人们可能会认为每种信息源可以传递任何信号,而不需要去管其它信号源如何进行信息传递。然而,
让两种信息源——其中一种信息源使用常规信号而另一种信号源使用反式信号——来传递同一类型的模糊信息
是毫无意义的。如果它们传递的是相同的信息,那么就应该使用同样类型的信号。传递的信息量不会因此而
减少,并且信号方法会更加简洁。
结论:要么都用常规信号,要么都用反式信号。
基于同样的理由,让信息源O和S传递相同的信息也是毫无意义的,因为这两种信息源传递信息的时间相同
(都是在第二墩牌),而且信号源O给出的是准确信息。因此我们有:SO ≠ SS。
另一方面,信息源F和信息源O可以用来传递相同的信息,因为这么做可以既保证速度(F),又保证准确性
(O)。信息源F和O之间的这种交互意味着我们可以更容易地判断第一墩打出的小牌到底 ↑ 是还是 ↓。
可分类体系的命名法
使用结构性定义,我们可以把小牌体系命名为SF SO SS。
在某花色的第二墩出牌时跟出最小牌的体系可以使用符号SF SO ↓,或者用
更简单的符号SF SO。
每种信息源都会被赋予一种特定的信号,然而给信息源S(第二张小牌)的信号通常会写于括号之中或
干脆被省略。
一些例子:
-
QML = 质量 - 混合(长度)信号体系
-
QL*↓ = 质量 - 反式长度信号体系
-
L*M = 反式长度 - 混合信号体系
在SF = SO的小牌体系里,前两种信号是相同的,例如:
-
QQM = 质量(混合)信号体系
-
MM↓ = 混合信号体系
-
L*L*Q = 反式长度(质量)信号体系
根据名称对体系的重建
以小牌体系QM为例:
-
信息源F: 传递质量信号Q,换句话说就是:
-
↓ = 好套(有一个大牌)
-
↑ = 坏套(上无大牌)
-
信息源O:传递混合信号M,换句话说就是:
-
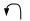 = 偶数张小牌
= 偶数张小牌
-
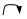 = 奇数张小牌
= 奇数张小牌
-
信息源S:↓(没有显式指明时默认为跟出最小牌张)
于是在小牌体系QM下,你应该使用如下出牌法:
务请注意↓并不总是表示你要跟出最小的牌张。更确切一点地说,是指和信息源O所传递的信号保持一致的最小
牌张。同样的理论也适用于↑。
各种不同的小牌体系
在这一章里,我们将会详细描述各种不同的小牌体系。它们可以分为三种类型:
-
传统或流行小牌体系
-
可分类小牌体系
-
“联合”小牌体系
传统或流行体系通常是不可分类的,它们是:
-
经典(CLA)
-
MUD(MUD)
-
反式(REV)
-
蓝队(BT)
-
桥牌杂志(JOU)
由于上述列表中的一些体系并非完全的小牌体系,换句话说就是对某些特定的持牌并没有清楚的定义应该引出
哪张牌,作者不得不对它们进行重建,同时对和信息源S有关的信号进行一些小的改动。可分类小牌体系从整体
来说是一种全新的方法,和传统体系没有任何联系。我们暂时还不来讨论“联合”体系,因为很多读者对它尚无
了解,而且它也不是可分类的。
经典体系(CLA)
这个体系着眼于快速的信息传递(第一墩牌)以显示该花色的质量:
-
↑ = 坏套(该花色全部由小牌组成)
-
↓ = 好套(该花色由一张大牌领头)
用更科学一点的术语来说就是,信息源F传递的是常规质量信号。信息源O通过同样传递常规质量信号的方式
来进一步确认信息源F传递的信息:
-
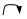 = 坏套
= 坏套
-
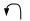 = 好套
= 好套
上述规则有一些例外,就是当你持有一张大牌领头的5或6张套的时候(稍后会进一步解释)。否则的话,
经典体系事实上等同于可分类体系中的质量体系(QQ↓),如下表所示:
“长四”约定
经典体系的对称性在持牌为一张大牌领头的5或6张套时被破坏。取而代之的是如下规则:
当从好套(至少4张并由一张大牌领头)中出牌时,引出第四大牌。这个方法的优越性在于:
-
让同伴知道自己在该花色中的长度,通过:
-
第二墩牌打出一张大于首攻牌张的小牌表示自己持有Hxx或Hxxx
-
第二墩牌打出一张小于首攻牌张的小牌表示自己持有Hxxxx或Hxxxxx
-
让同伴知道你有3张大于首攻牌张的牌。因此在如下局势中:
西首攻8,东可以充满信心地跟小牌,只要他认为同伴在该花色中至少有4张。
MUD体系(MUD)
经典体系的缺陷是常常无法区分同伴到底是从双张还是三张小牌中引牌,即使在头两轮出牌过后。为了
克服这一缺陷,人们发明了MUD体系,当从三张小牌中引牌时,先引出中间张,然后跟出最大的小牌。图示
如下:
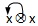
为了便于记忆,它被命名为MUD,其中:
-
M = Middle(中间)
-
U = Up(上面)
-
D = Down(下面)
这个设计能够有效地区分xx和xxx,同时也能区分xxx和xxxx(但仅仅是在第二墩牌打出之后)。当需要
鉴别引牌是从xxxx还是xxxxx,或者是从xxxxx还是xxxxxx中引出时,此时我们没有足够信息,似乎
以使用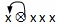 为佳。
为佳。
反式体系(REV)
反式体系和经典体系完全不同,介绍的是全新的思想:
反式体系的特征之一是绝对不首攻该花色中最大的牌张,因此如果你能看见所有比首攻牌张大的牌,
你就能肯定首攻是一个单张!然而这个推论并非如你想象的那样有用,毕竟出现此类局势的频率
非常之低。不首攻最大牌张的更重要作用是让同伴知道你只有一张牌比首攻牌张大(除了从长四
中引出的情况)。反式体系最大的弱点是即使两墩牌后,它仍不能区分xxx和Hxx。
“长三/长五约定”
先来看看在经典体系和MUD体系里使用的长四首攻:
这种处理方式意味着你能区分Hxxx和Hxxxx,但却无法知道同伴是Hxx还是Hxxx,或是Hxxxx还是Hxxxxx。一个
有效的补救方法是采用长三/长五首攻:
通过使用这种首攻,我们既可以区分该花色的长度,同时还保留了经典体系中“↓ = 好套”的含义。
不像长四首攻里有3张牌大于首攻牌张,长三首攻告诉同伴自己只有两张牌比首攻牌张大,从而使得
同伴在需要决定押上大牌或者忍让时更加容易准确判断。
蓝队体系(BT)
这个体系实质上是一个修订过的MUD体系,用“长三/长五”取代了“长四”。
蓝队体系有很强的逻辑性和对称性:
-
信息源F——传递信号Q
-
信息源O——传递信号L
-
信息源S——等价于↓
唯一的例外是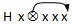 。如果用
。如果用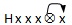 来取代它,则蓝队体系就等同于可分类体系QL(质量-长度)。由此我们可以得出结论,蓝队体系是
经典体系进化阶梯中的最高一级。
来取代它,则蓝队体系就等同于可分类体系QL(质量-长度)。由此我们可以得出结论,蓝队体系是
经典体系进化阶梯中的最高一级。
桥牌杂志体系(JOU)
在对抗无将定约时它几乎等同于QQ(质量)体系。但在对抗花色定约时的首攻如下表所示:
如你所见,对抗花色定约,桥牌杂志体系在持好套和坏套时都采用长三/长五首攻。它类似于
可分类体系的↓LQ。
注意,桥牌杂志首攻的原始资料没有提及第二墩牌的具体出法。作者在这里假设,只要有可能,
信息源S传递的是质量信号Q。
可分类体系
现在我们来详细分析各种可分类体系,换句话说,可以用结构性定义来描述的小牌体系。它们
分成两个大类:
-
SF = SO的体系:
|
QQL/QQM(简称为QQ)
|
LLQ/LLM(简称为LL)
|
MML/MMQ(简称为MM)
|
-
SF ≠ SO的体系:
|
QLQ/QLM(简称为QL)
|
QMQ/QML(简称为QM)
|
|
LQL/LQM(简称为LQ)
|
LML/LMQ(简称为LM)
|
|
MQL/MQM(简称为MQ)
|
MLM/MLQ(简称为ML)
|
我们在上面只列出了使用常规信号的体系;注意反式信号和常规信号在实质上是等价的,因此没有必要将
使用反式信号的体系也一一列出。
下面是所有可分类体系的引牌法图解:
“联合”小牌体系(C)
虽然联合小牌体系是不可分类体系,它还是有一定的规律性:
-
信息源F:
-
↓ = 攻击性首攻(由一张大牌领头的花色或双张中引出)
-
↑ = 消极性首攻(从xxx之类的花色中引出)
-
当从三张或更多的小牌中引出时和QQL体系相同(xxxxxx稍有区别)
-
当从一张大牌领头的花色中引出时和QL体系相同(Hxxxxx稍有区别)
对联合体系更具体的描述请看第三章。
此后的分析过于理论化,决定予以省略。作者将各种体系的有效性予以量化并得出如下结论:
各种小牌体系的最终有效性
| 1) |
79.56% |
C(联合) |
| 2) |
77.75% |
ML(混合-长度) |
| 3) |
77.20% |
MM(混合) |
| 4) |
76.94% |
QM(质量-混合) |
| 5) |
76.56% |
MQ(混合-质量) |
| 6) |
76.23% |
QQ(质量)/LL(长度) |
| 7) |
75.58% |
CLA(经典) |
| 8) |
75.37% |
REV(反式) |
| 9) |
74.40% |
BT(蓝队) |
| 10) |
74.38% |
QL(质量-长度)/LQ(长度-质量) |
| 11) |
73.09% |
LM(长度-混合) |
| 12) |
72.50% |
MUD |
| 13) |
70.37% |
JOU(桥牌杂志) |